First principles exploration 👋
The goal of this article is to explore the topic of the camera response function experimentally. We’ll build up from first principles and the main focus will be on building intuition with code examples. The only pre-requisite is base familiarity with Python + NumPy and, of course, curiosity about the topic. 🧑🚀
If you’re looking for a quick way to find out the response function of your camera, you can check out the implementation of CalibrateDebevec in OpenCV, or stick around to get a deeper intuition.
I’ve made an effort to link to interesting resources that provide a good starting point to dig deeper into specific directions that could not be covered in this article. You’re encouraged to follow them and come back to this at your own pace.
What the CRF? 🤔
A camera measures the light intensity hitting the imaging sensor and outputs an image with pixel values that in some way correspond to that light intensity. This correspondence is modeled by the camera response function (CRF).

For a computer vision engineer, the pixel values are the only observation of the real-world. Thus, it is helpful to understand how they relate to actual light intensities to correctly model that world.
Most cameras have some non-linearity in their response to light intensities. Images taken by consumer-grade cameras are particularly affected by this because they are optimized for viewing experience and not for measurement accuracy.
Applications of the CRF 🔨
Many computer vision algorithms that rely on the brightness constancy assumption require accurate estimation of the CRF. For example, optical flow or any direct method for visual SLAM that works with pixel intensities such as DSO.
Direct methods for visual SLAM are currently one of the most robust approaches for accurate robot localization in challenging environments where GNSS coverage is unreliable. An autonomous last-mile robot delivery service is an example that’s increasingly gaining commercial traction in recent years and may use such technology.

In this article, we’ll look at the application of generating HDR images which also relies on knowledge about the camera response function because we need to “fuse” multiple images taken at different exposure times.
How cameras measure light ☀️
A camera is an array of photodiodes that converts incoming photons into electrical current or voltage. This phenomenon is known as the photoelectric effect and is the same phenomenon utilized in solar panels.
For each pixel, there’s a corresponding photodiode in the camera sensor. We take an image by exposing the sensor to light for a given period (exposure time). Since the photodiodes produce an electrical current proportional to the amount of light they receive, we can use that measurement to reconstruct the image.

Converting voltages to pixel values 📺
When we measure the voltage generated by the photodiode we get an analog quantity. But we need a digital value that fits into our pixel representation of 8 bits. A device that can perform this conversion is called an Analog-Digital (A/D) converter. Most A/D converters used in cameras today will output an 8, 12, or 16-bit digital value.
Analog-to-Digital Converter 📈
We will start with an 8-bit A/D converter. Note that regardless of the bit depth, the range of possible values will be limited in the digital domain. Meaning that with 8-bit we only have \(2^{8} = 256\) , unique values to assign to all possible voltage measurements.
Let’s simulate a naive A/D converter:
def max_value(bit_depth: int) -> int:
"""Return max integer value for the specified bit depth"""
return 2**bit_depth - 1
def adc(milivolts: np.ndarray, bit_depth: int = 8) -> int:
"""Naive A/D converter
milivolts -- accumulated voltage from a photodiode
bit_depth -- target bit depth of the digitized output
"""
return np.clip(np.around(milivolts), 0, max_value(bit_depth))
def plot_adc_examples():
"""Plot a few interesting examples"""
f, axes = plt.subplots(1, 3, figsize=(20, 5))
x_label = 'Input voltage (mV)'
y_label = 'Output pixel value'
voltages = np.arange(0, 10, 0.1)
util.plot(axes[0], voltages, adc(voltages),
"In supported range", x_label, y_label)
voltages = np.arange(0, 0.5, 0.01)
util.plot(axes[1], voltages, adc(voltages),
"Below supported range", x_label, y_label)
voltages = np.arange(255, 500, 1)
util.plot(axes[2], voltages, adc(voltages),
"Above supported range", x_label, y_label)
plot_adc_examples()
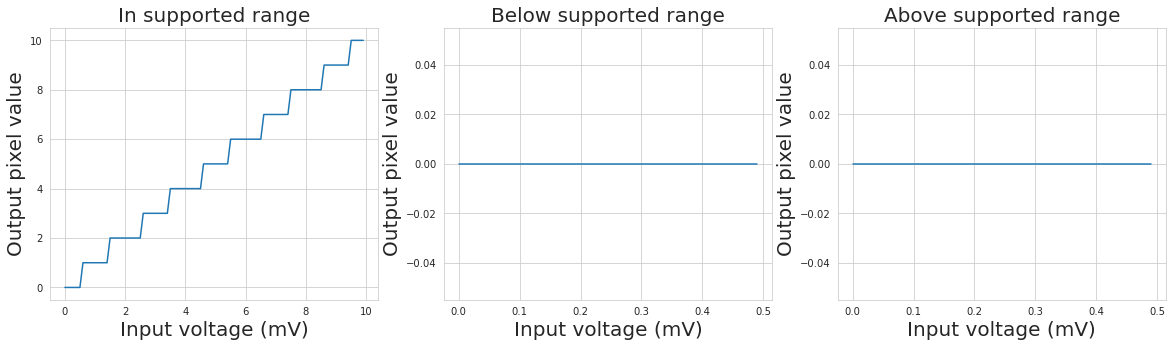
Quantization noise
From the staircase-like plot above we can see the discrete jumps caused by the quantization effects. Because we’re losing some precision at this step, this effect also becomes a component of the total image noise known as the quantization noise.
Under- and overexposure
The plot also demonstrates that any values below or above the supported range are irreversibly lost. This phenomenon is known as under- or overexposure. Our goal will always be to choose the exposure time such that this effect is minimized.
Dynamic Range
The range of light intensities that the camera can capture without under- or overexposure is called the camera dynamic range. It is a very important metric for outdoor robot operation due to the large variations in light intensities.
So our goal is to maximize the information we can get from every image. We have two ways to optimize for that:
- Choose a camera with a higher dynamic range
- Adjust the exposure time to minimize over- and underexposure
Programmable Gain Amplifier ⬛
Underexposure happens for dimly lit scenes or shorter exposure times when the photodiodes don’t have a chance to convert a sufficient amount of photons into electrical current. This is how a fully underexposed image looks:
photodiode_array_milivolts = np.array([0.028, 0.213, 0.234, 0.459])
pixel_values = adc(photodiode_array_milivolts)
util.display_images([pixel_values], titles=["Underexposed image"])

Cameras have a programmable-gain amplifier (PGA) that can amplify the voltages from the photodiodes and bring them in the range supported by the A/D converter. The level of amplification can be configured on most cameras through the ISO setting.
def pga(milivolts: np.ndarray, gain: float = 1.0) -> float:
"""Naive programmable-gain amplifier
milivolts -- input voltage from photodiode
gain -- ratio output / input
"""
return gain * milivolts
# Add an amplifier to the same example values from above
pixel_values = adc(pga(photodiode_array_milivolts, gain=300.0))
util.display_images([pixel_values], titles=["Amplified image"])

There’s a caveat: we did not model image noise. The weaker signal in dimply lit scenes results in a lower signal-to-noise ratio (SNR). In other words, amplifying the signal will also amplify the noise and that’s why using a higher gain usually results in grainier and lower quality images. In extreme cases when the strength of the signal is below the noise floor it can be difficult to extract any useful information.
Reducing the image noise can be performed in the digital image processing pipeline which is the final step before saving the image. This part significantly differs between camera models and may include white balance, tone mapping, gamma encoding, image compression and more.
Image Acquisition Pipeline 📸
The figure below provides an overview of the discussed components.

Further Recommended Reading 📚
I’m aware that I’ve touched upon a lot of topics very quickly. If you don’t have a good intuition already, I highly recommend reading this amazing interactive introduction on Cameras and Lenses. Seriously, please go check this article out.
The Science of Camera Sensors is another great resource in video form that provides an excellent introduction to the physics of how photodiodes and camera sensors work.
Advanced: For a more in-depth look into the theory and physics behind CMOS photodiodes, chapter 3 from this dissertation provides a good overview.
Simulating a simple camera 📷
Disclaimer ℹ️
For the sake of brevity, many of the physical aspects of cameras are oversimplified in the presented examples. They are only meant to aid the intuition and shouldn’t be relied upon for accuracy or completeness. However, if you spot any mistakes, I would love to hear about them at 📨 or on X.
Assumptions 📝
Camera
- uses the pinhole camera model — i.e. no modeling of camera optics
- is monochrome — i.e. no simulation of the color filter array and demosaicing
- 8-bit grayscale output format is used for the images
- static camera — there’s no motion during or between image acquisitions
Scene
- receives constant light intensity from the light source (brightness constancy)
- static — no moving objects in the scene during or between image acquisitions
In a practical sense, it means that we cannot accurately determine the camera response function on a partly cloudy day while relying on sunlight as our light source because the clouds may result in significant changes in the radiant flux received by the scene.
Simulating a 2x2 pixel sensor 🧱
We will use the term pixel irradiance to refer to the number of photons hitting the physical area of a pixel per second ( \(m^{−2}⋅s^{−1}\) ). You can also refer to SI photon units definition on the wiki page of photon counting.
import numpy as np
def get_sensor_irradiance():
"""Get a sample sensor irradiance
We have an imaging sensor of 2x2 pixels (stored as 1D array)
The sensor irradiance encodes how many photons
are hitting the image sensor every second.
The values are arbitrarily chosen.
"""
pix11_irradiance = 1122 # photons / second
pix12_irradiance = 3242 # photons / second
pix21_irradiance = 1452 # photons / second
pix22_irradiance = 25031 # photons / second
return np.array([
pix11_irradiance, pix12_irradiance,
pix21_irradiance, pix22_irradiance])

Let’s start with the simple case of a linear camera response function. This intuitively means that doubling the amount of light (pixel irradiance) would result in doubling the observed pixel value. We define the CRF as:
$$CRF = G(x) = a\cdot x + b$$
We’re going to set \(a = 1\) and \(b = 0\) and assume that each photon increases the voltage by 1mV. This is easy to simulate but unfortunately, 100% detached from reality. Accurate simulation of that process is not in the scope of the article but feel free to enter that rabbit hole starting from quantum efficiency ;-). We also assume white Gaussian noise which approximates thermal noise. All other sources of noise will be ignored.
$$CRF = G(x) = x$$
To get an estimate of the voltage accumulated in each pixel, we need to integrate the irradiance over the period of the exposure time t. We define taking an image as:
where E is the sensor irradiance (i.e. an array of all pixel irradiances), G is the camera response function as already defined above, t is the exposure time in seconds, I is the image intensity or observed pixel value and k is the index of the pixel.
In the literature, you may find the equation defined in its simpler form:
$$I(k) = G^{*}(t\cdot E(k))$$
where the camera response function is:
$$G^{*}(x) = G(adc(pga(x))$$
I’ve chosen to keep the functions separate here so that the logic for amplification and quantization is not intermingled with the CRF in the Python code.
Let’s code this:
from typing import Callable
ResponseFunction = Callable[[np.ndarray, int], np.ndarray]
def capture_image(E: np.ndarray, t: float, G: ResponseFunction,
bit_depth: int = 8, std_noise: float = 1.0) -> np.ndarray:
"""Simulate capturing an image with exposure time t.
You can specify higher bit_depth for internal processing prior to
finally converting the image to 8-bit depth before output.
E -- sensor irradiance
t -- exposure time (seconds)
G -- camera response function (CRF)
bit_depth -- bit depth for A/D converter output and response function input
std_noise -- standard deviation for the Gaussian noise distribution
"""
# Non-realistic but simple calculation
accumulated_milivolts = E * t
# Add the white Gaussian noise
noise = np.random.normal(0, std_noise, size=len(accumulated_milivolts))
accumulated_milivolts += noise
image = G(
adc(pga(accumulated_milivolts), bit_depth), bit_depth
)
# Always convert to 8-bit depth prior to saving / outputting
to_8bit_depth = max_value(8) / max_value(bit_depth)
return np.around(image * to_8bit_depth)
def linear_crf(X: np.ndarray, bit_depth: int) -> np.ndarray:
"""Linear camera response function G(x) = x"""
return X
Now take a couple of images with different exposures:
img1 = capture_image(E=get_sensor_irradiance(), t=1/10, G=linear_crf)
img2 = capture_image(E=get_sensor_irradiance(), t=1/100, G=linear_crf)
util.display_images([img1, img2],
titles=["Exposure: t = 1/10 second",
"Exposure: t = 1/100 second"])

We can correctly expose all pixels with 1/100 second exposure time (none of the pixels are 0 or 255). It becomes more interesting if we have a scene with more extreme values which cannot be captured by the dynamic range of the camera sensor.
Think of an image from inside a cave looking out.

We can simulate this by choosing more extreme values for the sensor irradiance:
def get_extreme_sensor_irradiance():
# Note that the range spans multiple orders of magnitude
return np.array([182, 5432, 15329, 252531])
t1, t2 = 1/5, 1/500
img1 = capture_image(E=get_extreme_sensor_irradiance(), t=t1, G=linear_crf)
img2 = capture_image(E=get_extreme_sensor_irradiance(), t=t2, G=linear_crf)
util.display_images([img1, img2],
titles=["Exposure: t1 = 1/5 second",
"Exposure: t2 = 1/500 second"])

In this example, it is not possible to capture the scene without loss of information regardless of the chosen exposure time. Correctly exposing the brightest pixel(s) will result in underexposing the darkest pixel(s) and vice versa. Note that in the second image we have one underexposed and one overexposed pixel.
Feel free to download the notebook and try it for yourself.
HDR Images 🪂
The pixel values provide us only partial information due to the limited dynamic range of the camera. To reconstruct an HDR image, we need to recover the full sensor irradiance.
Inverse CRF 🔙
The inverse camera response function allows us to do precisely that. It defines the mapping from pixel values back to sensor irradiance or light intensity.

We define \(U := G^{-1}\) as the inverse of the CRF. Here we assume that G is monotonically increasing and thus invertible. That’s a fair assumption because cameras are mapping brighter scene regions to brighter image intensities.
Remember that we defined taking an image as \(I(k) = G(t\cdot E(k))\) . To go the other direction, we can apply the inverse function \(U(I(k)) = t\cdot E(k)\) and we can get the sensor irradiance E from the image I if we know the exposure time t:
The inverse CRF is also identity function \(f(x) = x\) because:
$$U(G(x)) = x$$
Recover Image Irradiance 🖼️
InverseResponseFunction = Callable[[np.ndarray], np.ndarray]
def recover_image_irradiance(I: np.ndarray,
t: float, U: InverseResponseFunction) -> np.ndarray:
"""Recover the irradiance from an image that was
taken with known exposure time t.
We cannot recover any useful information from
oversaturated (255) or undersaturated (0) image
intensities. Return 0 in both cases as this helps
eliminate the need for separate case handling.
I -- image (array of image intensities)
t -- exposure time (seconds)
U -- inverse of the response function
"""
I[I == 255] = 0 # oversaturated pixels
return U(I) / t
def linear_inverse_crf(I: np.ndarray) -> np.ndarray:
"""Linear inverse camera response function U(x) = x"""
return I
print(f"\nImage irradiance (t = {t1}):")
print(recover_image_irradiance(I=img1, t=t1, U=linear_inverse_crf))
print(f"\nImage irradiance (t = {t2}):")
print(recover_image_irradiance(I=img2, t=t2, U=linear_inverse_crf))
Image irradiance (t = 0.2): [185. 0. 0. 0.]
Image irradiance (t = 0.002): [ 0. 6000. 15000. 0.]
Notice that we can recover the irradiance only for pixels that are not under- or overexposed. To recover the full sensor irradiance, we need to capture a series of images with different exposure times such that each pixel was correctly exposed at least once.
Let’s take another image with a shorter exposure time:
t3 = 1/2000
img3 = capture_image(E=get_extreme_sensor_irradiance(), t=t3, G=linear_crf)
print(f"\nImage irradiance (t = {t3:.4f}):")
print(recover_image_irradiance(I=img3, t=t3, U=linear_inverse_crf))
Image irradiance (t = 0.0005): [ 0. 6000. 16000. 254000.]
Recover Sensor Irradiance 📷
We can now estimate the full sensor irradiance by combining the individual image irradiances. Notice that the second and the third image have a conflicting estimate of the third pixel value (15000 vs 16000). We’re going to take the average.
from typing import List
def estimate_sensor_irradiance_average(images: List[np.ndarray],
exposures: List[float],
U: InverseResponseFunction) -> np.ndarray:
"""Recover the sensor irradiance
images -- list of images to use for recovery
exposures -- corresponding list of exposures
U -- inverse response function
"""
assert len(images) == len(exposures), \
"The number of images and exposures don't match"
assert len(images) > 0, "Expected non-empty list of images"
image_size = images[0].shape[0]
irradiance_sum = np.zeros(image_size)
irradiance_count = np.zeros(image_size)
for I, t in zip(images, exposures):
image_irradiance = recover_image_irradiance(I, t, U)
irradiance_sum += image_irradiance
# Only non-zero values are observed and contribute to average
irradiance_count[image_irradiance != 0] += 1
return np.divide(irradiance_sum, irradiance_count,
out=np.zeros(image_size),
where=irradiance_count != 0)
Let’s compare that to the known ground-truth.
estimated_sensor_irradiance = estimate_sensor_irradiance_average(
[img1, img2, img3], [t1, t2, t3], U=linear_inverse_crf)
util.print_error_to_ground_truth(
estimated_sensor_irradiance, ground_truth=get_extreme_sensor_irradiance())
Ground-truth: [ 182 5432 15329 252531]
Estimated: [ 180. 6750. 13750. 248000.]
Error (diff): [ 2. -1318. 1579. 4531.]
It seems we’re close but have lost some precision due to quantization effects and image noise. Can we do better? Maybe average over more images?
Improving the sensor irradiance estimate
In this section, we run several experiments to better understand how the noise affects the accuracy. First, we need a more representative dataset with more images.
from typing import Tuple, List
ImagesExposuresTuple = Tuple[List[np.ndarray], List[float]]
def generate_sliding_exposure_dataset(
E: np.ndarray, G: ResponseFunction, bit_depth: int = 8,
start_us: int = 40, step_perc: int = 5, number_exposures: int = 220,
images_per_exposure: int = 1) -> ImagesExposuresTuple:
"""Generate dataset with sliding exposure values
E -- sensor irradiance
G -- camera response function
bit_depth -- bit depth for the camera's internal processing
start_us -- microseconds for the starting value of the sequence
step_perc -- percentage step between subsequent exposure values
number_exposures -- number of unique exposure times to generate
images_per_exposure -- number of images per exposure time
"""
def get_exposure_seconds(idx: int) -> float:
multiplier = (1 + (step_perc / 100)) ** idx
return round(start_us * multiplier) * 1e-6
images, exposures = [], []
for exposure_idx in range(number_exposures):
for _ in range(images_per_exposure):
t = get_exposure_seconds(exposure_idx)
images.append(capture_image(E=E, t=t, G=G))
exposures.append(t)
return images, exposures
Feel free to experiment with the parameters for the dataset generation and see what the impact on the final sensor irradiance estimates is.
images, exposures = generate_sliding_exposure_dataset(
E=get_extreme_sensor_irradiance(), G=linear_crf)
util.display_valid_observations(np.array(images))

Following, I define a helper function that will help us quickly run a few experiments.
EstimateSensorIrradianceFunction = Callable[[List[np.ndarray], List[float],
InverseResponseFunction], np.ndarray]
def get_irradiance_estimates(
estimate_func: EstimateSensorIrradianceFunction,
images_per_exposure: int,
number_experiments: int) -> List[np.ndarray]:
"""Get sensor irradiance estimates from a number of experiments"""
estimates = []
for _ in range(number_experiments):
images, exposures = generate_sliding_exposure_dataset(
E=get_extreme_sensor_irradiance(), G=linear_crf,
images_per_exposure=images_per_exposure)
irradiance_estimate = estimate_func(
images, exposures, U=linear_inverse_crf)
estimates.append(irradiance_estimate)
return estimates
Let’s run 10 experiments with a single image per exposure time.
irradiance_estimates = get_irradiance_estimates(
estimate_sensor_irradiance_average,
images_per_exposure=1, number_experiments=10)
util.plot_errors_to_ground_truth(
irradiance_estimates, ground_truth=get_extreme_sensor_irradiance())
RMSE: 1425.4632661240885

Now we have a baseline of root-mean-square error (RMSE) that we want to minimize. I’ve also plotted the per-pixel RMSE and the per-experiment absolute error for the estimate.
rradiance_estimates = get_irradiance_estimates(
estimate_sensor_irradiance_average,
images_per_exposure=10,
number_experiments=10)
util.plot_errors_to_ground_truth(
irradiance_estimates, ground_truth=get_extreme_sensor_irradiance())
RMSE: 1215.9117041699783

The vertical oscillations have now subsided and the RMSE is slightly improved.
Notice that the errors for most pixels, except the fourth (red in the figure), are biased toward negative values. This is not caused by the image noise because we would otherwise expect a mean error of zero.
Let’s plot the distribution of the observations that we have for each pixel.
util.display_observations_distribution(np.array(images))
![]()
Now we see that the observations in our dataset are similarly skewed. The fourth pixel which had the smallest bias in the estimate also has the best observation distribution.

The skewed observations are the result of using a geometric sequence for the exposure times. In our case it looks like this:
util.plot_exposures(exposures)

The geometric progression is convenient here due to the large range of values we need to cover. We are able to do so with just over 200 exposures. If we use an arithmetic progression, on the other hand, we would need significantly more pictures in the dataset which is not always practical or possible.
Instead, we can improve the algorithm by adding a weighting function that discounts the contribution from observations with lower and higher pixel values.
I’m going to use the weighting function proposed by Debevek & Malik:
\[w(z) = \begin{cases} z - Z_{min} & \text{for } z\leq \frac{1}{2}(Z_{min} + Z_{max})\\ Z_{max} - z & \text{for } z\gt \frac{1}{2}(Z_{min} + Z_{max}) \end{cases}\]where \(Z_{min}\) and \(Z_{max}\) are the least and greatest pixel values — 0 and 255 respectively.
\[w(z) = \begin{cases} z & \text{for } z\leq 127\\ 255 - z & \text{for } z\gt 127 \end{cases}\]This function discounts both lower and higher pixel values. Besides the higher robustness towards different noise sources (see also CCD Saturation and Blooming), it also reflects the fact that values in the mid-range are most accurately encoded by non-linear camera response functions (more on this later).
def weighting_debevek_malik(pix_value: int) -> int:
"""Weighting function for recovering irradiance"""
if pix_value <= 127:
return pix_value
if pix_value > 127:
return 255 - pix_value

Let’s rewrite the function for sensor irradiance estimation to use the weighting function:
def estimate_sensor_irradiance_weighted(
images: List[np.ndarray], exposures: List[float],
U: Callable[[np.ndarray], np.ndarray], w: Callable[[int], int]) -> np.ndarray:
"""Estimate the sensor irradiance
The recovered image irradiances are weighted according to the provided
weighting function. This works best with higher number of images
and well-distributed exposure times.
images -- list of images to use for recovery
exposures -- corresponding list of exposures
U -- inverse response function
w -- weighting function
"""
assert len(images) == len(exposures), \
"The number of images and exposures don't match"
assert len(images) > 0, "Expected non-empty list of images"
image_size = images[0].shape[0]
w_vec = np.vectorize(w)
irradiance_sum = np.zeros(image_size)
irradiance_count = np.zeros(image_size)
for I, t in zip(images, exposures):
weights = w_vec(I)
image_irradiance = recover_image_irradiance(I, t, U)
irradiance_sum += weights * image_irradiance
# Only non-zero values are observed and contribute to average
irradiance_count[image_irradiance != 0] += weights[image_irradiance != 0]
return np.divide(irradiance_sum, irradiance_count,
out=np.zeros(image_size),
where=irradiance_count != 0)
RMSE: 165.4355269685378

This change alone provides an almost 10x improvement in the estimate errors. I found out that using the square of the weighting function provides even better results.
def weighting_squared(pix_value: int) -> int:
return weighting_debevek_malik(pix_value) ** 2

RMSE: 72.49150623466912

And here’s the final estimate:
images, exposures = generate_sliding_exposure_dataset(
E=get_extreme_sensor_irradiance(), G=linear_crf)
recovered_sensor_irradiance = estimate_sensor_irradiance_weighted(
images, exposures, U=linear_inverse_crf, w=weighting_squared)
util.print_error_to_ground_truth(
recovered_sensor_irradiance, ground_truth=get_extreme_sensor_irradiance())
Ground-truth: [ 182 5432 15329 252531]
Estimated: [ 184.362 5436.691 15341.962 252564.875]
Error (diff): [ -2.362 -4.691 -12.962 -33.875]
Absolute vs Relative Irradiance ⚠️
Recovering the absolute sensor irradiance isn’t quite as straightforward for real cameras. We’ve used a very simplified model of capturing images and haven’t taken the photodiode’s quantum efficiency and other physical aspects into consideration.
Although it may seem that we fully recovered the irradiance values, this method can only recover the relative irradiance values up to an unknown constant factor \(X\) .
$$ E_{absolute} = X \cdot E_{relative} $$
To determine \(X\) , an absolute radiometric calibration can be performed. The process involves taking an image of a surface with known reflectance values in a controlled light environment.
Conveniently, the relative irradiance values that we obtained are sufficient for most applications, including HDR images.
Displaying HDR Images 🖥️
We could display the HDR image by normalizing the values within the 0-255 range.
def normalize_255(image: np.ndarray) -> np.ndarray:
"""Normalize values withing range [0, 255]"""
min_i, max_i = min(image), max(image)
assert min_i < max_i, "Range cannot be normalized (min == max)"
return np.around((image - min_i) * (255 / (max_i - min_i)))
hdr_linear = normalize_255(recovered_sensor_irradiance)
util.display_images([hdr_linear], titles=["HDR (linear)"])

After normalization, the darkest and brightest pixels are pinned to the values of 0 and 255 respectively. All other values are linearly adjusted. The problem with this method is that usually the scene will have very few but extremely bright spots and this would cause the majority of the rest of the scene to appear underexposed.
The image above is a good example of this effect.
This is a limitation of the display technology today. Most devices still have a non-HDR display which is only capable of displaying 24-bit color which is exactly 8-bit per RGB channel. This sets a hard limit on the range of values [0-255].
Gamma encoding 📈
To go around this problem cameras perform gamma encoding when saving images in 8-bit format. In doing so, the limited range can be utilized more efficiently.
def gamma(X: np.ndarray) -> np.ndarray:
assert all(X >= 0) and all(X <= 1)
return X**(1/2.2)
def plot_gamma_function():
plt.title("Linear vs Gamma")
plt.xlabel("Input")
plt.ylabel("Output")
x = np.arange(0, 1, 0.001)
plt.plot(x, gamma(x))
plt.plot(x, x)
plot_gamma_function()

The gamma function encodes lower values (darker tones) with significantly higher resolution. This mapping exploits the fact that our eyes perceive brightness proportionally to the logarithm of the light intensity. See Weber-Fechner law.
Think of a light bulb with adjustable brightness. If we increase the light intensity by N two consecutive times, the perceived brightness change will be larger the first time.

The gamma encoding is reversed by a gamma decoding step which applies the inverse of the gamma function. Your monitor likely expects gamma encoded images and automatically does the decoding. All of this is formally defined in the sRGB color space.
Note that the gamma function is just one of many possible tone mapping techniques. We are not going to cover more, but I highly recommend this great article on color spaces.
For very high dynamic range images you can also take the logarithm and normalize the resulting values over the [0-255] range. Following is an example of both approaches.
def apply_gamma(E: np.ndarray, bit_depth: int = 8):
return gamma(E / max_value(bit_depth)) * max_value(bit_depth)
hdr_gamma = apply_gamma(normalize_255(recovered_sensor_irradiance))
hdr_log = normalize_255(np.log(recovered_sensor_irradiance + 1))
util.display_images([hdr_linear, hdr_gamma, hdr_log], titles=["HDR (linear)", "HDR (gamma)", "HDR (log)"])

Non-linear CRF 🎛️
Up to now, we’ve assumed that the CRF is linear \(G(x) = x\) . However, we’ve seen that it makes sense for cameras to encode images using a non-linear curve to optimize for dynamic range and appearance.

Additional non-linearities might be introduced by other parts of the system — e.g. the A/D converter or other digital image processing steps such as white balance correction. The goal of the CRF calibration is to find the overall response of the camera that combines all these factors into a single function.

CRF Calibration 🔬
In this section, we’re going to implement a simple but effective algorithm for determining the camera response function from a set of monochrome images. The algorithm is inspired by the approach presented in the paper: A Photometrically Calibrated Benchmark For Monocular Visual Odometry.
Calibrate from a single pixel 💡
Let’s iteratively discover the approach by first considering an image consisting of 1 pixel.

Given our assumptions about the scene, we have full control over the amount of light that a pixel receives by controlling the exposure time. We don’t know the absolute value but we know that if we double the exposure time, we receive double the amount of light.
The inverse CRF takes a pixel value as an argument and we know that pixel values are integers in the range [0-255]. So we can define it as a discrete function. In Python, this translates to an array where the index of the array is the input to the function.
U = np.array([0.] * 256)
We need to have observations for each possible pixel value to fully determine the inverse CRF. So our calibration dataset needs to start from a fully underexposed image and iteratively increase exposure time until the image is overexposed.
Here it makes more sense to use arithmetic progression for the exposures so that we have dense coverage over the entire range.
def generate_crf_calibration_dataset(
E: np.ndarray, G: Callable[[np.ndarray, int], np.ndarray],
bit_depth: int = 8, start_ms: int = 1, end_ms: int = 201,
step_ms: int = 1, images_per_exposure: int = 1) -> ImagesExposuresTuple:
"""Generate dataset with sliding exposure values in the specified range
E -- sensor irradiance
G -- camera response function
bit_depth -- bit depth for the A/D converter of the camera
start_ms -- start value (ms) for the range of exposure values
end_ms -- end value (ms) for the range of exposure values
step_ms -- step size (ms) for the range of exposure values
images_per_exposure -- number of images per exposure time
"""
exposures = [x / 1e3 for x in range(start_ms, end_ms, step_ms)]
exposures *= images_per_exposure
images = []
for t in exposures:
images.append(capture_image(E=E, t=t, G=G, bit_depth=bit_depth))
return images, exposures
Recovering linear response
As a first example, we’re going to generate a dataset using the linear response function and attempt to recover it. We use an arbitrarily chosen pixel irradiance:
single_pixel_irradiance = np.array([1381])
Generate the dataset and verify that it provides a good distribution of pixel values.
images, exposures = generate_crf_calibration_dataset(
E=single_pixel_irradiance, G=linear_crf)
util.display_images(images[0::10], shape=(1,1), annot=False)
![]()
util.display_observations_distribution(np.array(images))
![]()
We don’t have sufficient images to cover every value from the range (200 images vs 256 values) but we have good enough coverage. Reality isn’t perfect either so let’s try to work around that and recover the reverse CRF function U.
$$U(I(x)) = t\cdot E(x)$$
def recover_U_single_pixel(exposures, images):
# Define an arbitrary (relative) sensor irradiance
# Expected to be wrong by a constant factor X
sensor_irradiance = np.array([100])
# Initialize the inverse function U to 0s
U = np.array([0.] * 256)
for t, image in zip(exposures, images):
pixel_value = int(image[0])
if pixel_value == 255 or pixel_value == 0:
# Skip under- or overexposed pixels
continue
accumulated_photons = t * sensor_irradiance[0]
U[pixel_value] = accumulated_photons
return U
util.plot_inverse_crf(recover_U_single_pixel(exposures, images))

The zero values are caused by unobserved pixel values. One way we can resolve that is by taking more images with finer exposure steps to cover the entire range of values.
Then we get a very good approximation without stricter requirements on the dataset.
def interpolate_missing_values(U):
observed_intensity = np.zeros(len(U), dtype=bool)
observed_intensity[U != 0.0] = True
U[~observed_intensity] = np.interp(
(~observed_intensity).nonzero()[0],
observed_intensity.nonzero()[0],
U[observed_intensity])
return U
util.plot_inverse_crf(
interpolate_missing_values(
recover_U_single_pixel(exposures, images)))

The recovered function looks a bit noisy. Debevek & Malik propose adding a smoothness term based on the sum of squared second derivatives.
# Create a dataset with multiple images for each exposure time
images, exposures = generate_crf_calibration_dataset(
E=single_pixel_irradiance, G=linear_crf, images_per_exposure=20)
def recover_U_single_pixel_average(exposures, images):
sensor_irradiance = np.array([100])
U_sum = np.array([0.] * 256)
U_count = np.array([0] * 256)
for t, image in zip(exposures, images):
pixel_value = int(image[0])
if pixel_value == 255 or pixel_value == 0:
# Skip under- or overexposed pixels
continue
accumulated_photons = t * sensor_irradiance[0]
# Sum all observations for specific pixel value
U_sum[pixel_value] += accumulated_photons
U_count[pixel_value] += 1
# Calculate the average
observed_intensity = np.zeros(len(U_sum), dtype=bool)
observed_intensity[U_count != 0] = True
return np.divide(U_sum, U_count, out=np.zeros_like(U_sum),
where=observed_intensity)
recovered_inverse_crf_linear = interpolate_missing_values(
recover_U_single_pixel_average(exposures, images))
util.plot_inverse_crf(recovered_inverse_crf_linear)

Nice and smooth 😊 I call this a success. Let’s move onto more interesting examples!
Recovering gamma response
To have meaningful gamma encoding, we need to quantize the images with a 12-bit A/D converter which provides a higher dynamic range that we can then effectively compress down to 8-bit with the gamma encoding. Note that we use 12-bit depth for the camera internal processing but the result is still an 8-bit (gamma encoded) image.
images, exposures = generate_crf_calibration_dataset(
E=single_pixel_irradiance, G=apply_gamma, images_per_exposure=20, bit_depth=12,
start_ms=1, end_ms=3001, step_ms=15)
Note that I also had to increase the step size for the exposure sequence to cover the extended dynamic range of the 12-bit A/D converter while keeping the total number of exposures constant between the examples.
util.display_images(images[0:200:10], shape=(1,1), annot=False)
![]()
The gamma dataset (bottom) appears to follow a more linear progression compared to the linear dataset (top). That’s because your monitor does gamma decoding and wrongly displays non-gamma encoded images.
![]()
![]()
util.display_observations_distribution(np.array(images))
![]()
recovered_inverse_crf_gamma = interpolate_missing_values(
recover_U_single_pixel_average(exposures, images))
util.plot_inverse_crf(recovered_inverse_crf_gamma)


Calibrate from multiple pixels 🐣
As demonstrated in the previous section, it is possible to calibrate the camera response function by using a single pixel. The downside of this approach is that it requires a lot of images to densely cover the entire range of values and average out the noise — we took 20 images @ 200 unique exposures resulting in a total dataset size of 4000 images.
Let’s hypothetically consider the other extreme case:
The image would have 4096 pixels in total. That’s approximately the same number of pixels as in our dataset with single pixel images. Assuming there’s a good variation in the pixel irradiances, would this provide us with the same amount of information?
The answer is no because we wouldn’t know the relative irradiances between the pixels.
The catch is that we already need to know the CRF to recover the irradiance values, but the irradiance values are needed to recover the CRF. The chicken and the egg puzzle?
In the following equation, both \(U(x)\) and \(E(x)\) are unknown.
$$U(I(x)) = t\cdot E(x)$$
But we know they’re both constant so if fix one and solve for the other, we can iteratively converge to a solution. In other words, we’re going to attempt to evolve the chicken and the egg simultaneously! 🐣
def recover_U(E: np.ndarray, exposures: List[float], images: List[np.ndarray]):
"""Attempt to recover the inverse CRF (U)
Calculation based on the formula U(I(x)) = t * E(x)
where I(x), t and E(x) are given as arguments.
All observations for a given I(x) are summed up and
the average is calculated. Non-observed values are interpolated.
E -- sensor irradiance
exposures -- list of exposure times t (seconds)
images -- images
"""
U_sum = np.array([0.] * 256)
U_count = np.array([0] * 256)
for t, image in zip(exposures, images):
for i in range(len(image)):
pixel_value = int(image[i])
if pixel_value == 255 or pixel_value == 0:
continue # Skip under- or overexposed pixels
accumulated_photons = t * E[i]
# Sum all observations for specific pixel value
U_sum[pixel_value] += accumulated_photons
U_count[pixel_value] += 1
# Calculate U as the average of all observations
observed_intensity = np.zeros(len(U_sum), dtype=bool)
observed_intensity[U_count != 0] = True
U = np.divide(U_sum, U_count, out=np.zeros_like(U_sum),
where=observed_intensity)
return interpolate_missing_values(U)
def recover_U_and_E(exposures, images, iterations=5):
"""Attempt to solve for both the inverse CRF and the sensor irradiance
Given a dataset, perform a number of iterations by alternatingly solving
for U(x) and E(x) to check if they can converge to a solution.
"""
E = np.array([100] * len(images[0]))
U = np.array([0.] * 256)
response_function = lambda x: U[int(x)]
U_list = []
E_list = []
for _ in range(iterations):
U = recover_U(E, exposures, images)
U_list.append(U)
E = estimate_sensor_irradiance_weighted(
images, exposures,
U=np.vectorize(response_function),
w=weighting_debevek_malik)
E_list.append(E)
return U_list, E_list
Let’s generate the dataset:
images, exposures = generate_crf_calibration_dataset(
E=get_sensor_irradiance(),
G=apply_gamma,
images_per_exposure=5,
bit_depth=12,
start_ms=1,
end_ms=3001,
step_ms=15)
I’ve experimented with the parameters until I got good coverage of pixel values for each pixel in the image. Here are the first ten darkest images from the sequence:
util.display_images(images[0:10], annot=False)
![]()
And here’s a representation of the full (subsampled) dataset:
util.display_images(images[0:200:10], annot=False)
![]()
Now we optimize for both the irradiance image and the inverse response:
U_list, E_list = recover_U_and_E(exposures, images, iterations = 5);
Here are the inverse response functions after each iteration of the optimization:
util.plot_multiple_inverse_crf(U_list)

And the irradiance images after each iteration:
util.display_images([normalize_255(np.log(E + 1)) for E in E_list])

print("Normalized Ground-truth: ", normalize_255(get_sensor_irradiance()))
print("Normalized Estimate: ", normalize_255(E_list[-1]))
print("Error: ", normalize_255(
get_sensor_irradiance()) - normalize_255(E_list[-1]))
Normalized Ground-truth: [ 0. 23. 4. 255.]
Normalized Estimate: [ 0. 23. 4. 255.]
Error: [0. 0. 0. 0.]
This approach quickly converges to the correct solution for both U and E. It starts falling apart if we try it with the more extreme sensor irradiance values.
images, exposures = generate_crf_calibration_dataset(
E=np.array(get_extreme_sensor_irradiance()), G=apply_gamma,
images_per_exposure=5, bit_depth=12,
start_ms=1, end_ms=3001, step_ms=15)
util.display_images(images[0:10], annot=False)
util.display_images(images[0:200:10], annot=False)
![]()
![]()
U_list, E_list = recover_U_and_E(exposures, images, iterations=5);
util.plot_multiple_inverse_crf(U_list)
util.display_images([normalize_255(np.log(E + 1)) for E in E_list])


Nothing we can’t resolve by throwing 50 iterations at it 😉
U_list, E_list = recover_U_and_E(exposures, images, iterations=50);
util.plot_multiple_inverse_crf(U_list[::10])
util.display_images([normalize_255(np.log(E + 1)) for E in E_list[::10]])


print("Normalized Ground-truth: ", normalize_255(get_extreme_sensor_irradiance()))
print("Normalized Estimate: ", normalize_255(E_list[-1]))
print("Error: ", normalize_255(
get_extreme_sensor_irradiance()) - normalize_255(E_list[-1]))
Normalized Ground-truth: [ 0. 5. 15. 255.]
Normalized Estimate: [ 0. 5. 15. 255.]
Error: [0. 0. 0. 0.]
As we’ll see in the next section, real datasets aren’t quite as extreme and converge within a reasonable number of iterations. In this example, we have only 2x2 images so any extreme values constitute a large percentage of the total pixels. Real-world images might have larger extremes but are constrained to a smaller percentage of the image.
Calibrate from a real dataset 🎉
And finally, we get to test our algorithms on a non-simulated dataset acquired with an actual camera! Yay!
You can download the dataset that I’ve used from here: Monocular Visual Odometry Dataset. We’re going to be using only two sequences from the dataset: narrow_sweep3 and narrowGamma_sweep3.
If you want to create a calibration dataset for your camera, you need to be able to programmatically control the exposure time. The camera needs to be static and point towards a static scene with good variability in surface reflectances. Ideally, you want to have close to a flat histogram. The light source has to be constant — beware that LED lights usually are not! You can use sunlight on a non-cloudy day.
Once you have that, you can fix the gain of your sensor to the lowest value to minimize noise and swipe the exposure time ( \(t\) ) in small \(\Delta t\) steps from the minimum value until the image becomes fully or mostly overexposed — the same way we’ve done in our simulated datasets.
import os
from skimage import io
from skimage.measure import block_reduce
def load_dataset(path: str, with_downsample: bool = True,
block_size: Tuple[int, int] = (10, 10)):
"""Load dataset from the specified path
Subsambling the image size in order reduce the execution time
of the (unoptimized) example algorithms
path -- path to the dataset
with_downsample -- enable/disable downsampling
block_size -- block size that gets sampled down to 1 pixel
"""
image_folder = os.path.join(path, "images")
exposure_file = os.path.join(path, "times.txt")
gt_file = os.path.join(path, "pcalib.txt")
exposures, images = [], []
shape_original, shape_output = None, None
def downsample(image):
"""Do max sampling in order to avoid bias from overexposed values"""
return block_reduce(image, block_size=block_size, func=np.max, cval=0)
with open(exposure_file, "r") as f:
for line in f.readlines():
# Parse meta information and append to output lists
[idx, ts, exposure_ms] = line.strip().split(" ")
exposures.append(float(exposure_ms) * 1e-3)
# Load and downsamble image
image_original = io.imread(os.path.join(
image_folder, idx + ".jpg"), as_gray=True)
image_output = downsample(image_original) \
if with_downsample else image_original
images.append(image_output.flatten())
if shape_output is None:
shape_original = image_original.shape
shape_output = image_output.shape
print("Original size: " + str(shape_original) +
" Output size: " + str(shape_output))
ground_truth = None
with open(gt_file, 'r') as f:
ground_truth = [float(i) for i in f.readline().strip().split()]
return exposures, images, shape_output, ground_truth
Let’s load the (downsampled) linear response dataset:
exposures, images, shape, ground_truth = load_dataset(
path="data/calib_narrow_sweep3")
Original size: (1024, 1280) Output size: (103, 128)
util.display_images(images[::200], shape=shape, annot=False)

I’m going to use the calibration results provided with the Monocular Visual Odometry Dataset as a reference ground-truth.

Let’s attempt to calibrate:
U_list, E_list = recover_U_and_E(exposures, images, iterations=3);
util.plot_multiple_inverse_crf(U_list)
util.display_images([normalize_255(np.log(E + 1)) for E in E_list],
shape=shape, annot=False)


Let’s try it on the gamma encoded dataset as well.
exposures, images, shape, ground_truth = load_dataset(
path="data/calib_narrowGamma_sweep3")
Original size: (1024, 1280) Output size: (103, 128)
util.display_images(images[::200], shape=shape, annot=False)


U_list, E_list = recover_U_and_E(exposures, images, iterations=3);
util.plot_multiple_inverse_crf(U_list)
util.display_images([normalize_255(np.log(E + 1)) for E in E_list],
shape=shape, annot=False)


It is amazing to see how well it works even with 1/10 of the available information after subsampling the images from their original size of (1024, 1280) to (103, 128).
Final Words 🏁
Although simple in its concept, the camera response function lies at the intersection of sensor physics and digital image processing. This makes it a fascinating topic to explore in-depth as it can lead our curiosity to a variety of unexplored paths.
We’ve barely scratched the surface of camera sensor physics, simulation, noise models and applications of the CRF. This article should hopefully provide a convenient starting point for self-learning and further research.
